7-1 Shapes and Designs - Concepts and Explanation
Polygon
A shape formed by line segments so that each of the segments meets exactly two other segments, and all of the points where the segments meet are end points of the segments.
Example
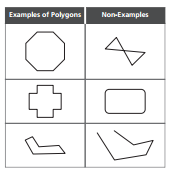
- Triangle 3 sides and 3 angles
- Quadrilateral: 4 sides and 4 angles
- Pentagon: 5 sides and 5 angles
- Hexagon: 6 sides and 6 angles
- Heptagon: 7 sides and 7 angles
- Octagon: 8 sides and 8 angles
- Nonagon: 9 sides and 9 angles
- Decagon: 10 sides and 10 angles
- Dodecagon: 12 sides and 12 angles
Regular Polygon
Polygons whose side lengths are equal and interior angle measures are equal.
Irregular Polygon
A polygon which either has two sides with different lengths or two angles with different measures.
Line (or mirror) Symmetry
Example
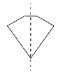
If the polygon is folded over the line of symmetry, the two halves of the shape will match exactly.
Rotational (or turn) Symmetry
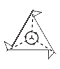
A polygon with turn symmetry can be turned around its center point less than a full turn and still look the same at certain angles of rotation.
Angles
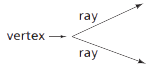
Angles are figures formed by two rays or line segments that have a common vertex. The vertex of an angle is the point where the two rays meet or intersect. Angles are measured in degrees.
Angle Measures
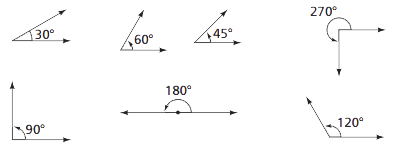
Work is done to relate angles to right angles, to develop students’ estimation skills. Combinations and partitions of 90° are used. 30°, 45°, 60°, 90°, 120°, 180°, 270°, and 360° are used as benchmarks to estimate angle size.
The need for more precision requires techniques for measuring angles. Students use an angle ruler or protractor to measure angles.
Angles and Parallel Lines
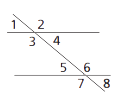
Students explore the angles created when two parallel lines are cut by a line. The line that cuts (intersects) the parallel lines is called a transversal. Angles 1 and 5, angles 2 and 6, angles 3 and 7, and angles 4 and 8 are called corresponding angles. Angles 4 and 5 and angles 3 and 6 are called alternate interior angles. Parallel lines cut by a transversal create equal corresponding angles and equal alternate interior angles.
Parallel lines and transversals help explain some special features of parallelograms such as the opposite angles have equal measures or that the sum of the measures of two adjacent angles is 180°.
Polygons that Tile a Plane
For regular polygons to tile a plane, the angle measure of an interior angle must be a factor of 360°.
Example
Only three regular polygons can tile a plane: an equilateral triangle (60° angles), a square (90° angles) and a regular hexagon (120° angles). There are also combinations of regular polygons that will tile, such as 2 octagons and a square.
Triangle Inequality Theorem
The sum of two side lengths of a triangle must be greater than the 3rd side length.
Example
![]() If the side lengths are a, b and c, then the sum of any two sides is greater than
the third: a + b > c, b + c > a, c + a > b
If the side lengths are a, b and c, then the sum of any two sides is greater than
the third: a + b > c, b + c > a, c + a > b