Page 7-2 Accentuate the Negative - Concepts and Explanation
Negative Numbers
Some subsets of the positive and negative numbers have special names.
Example
The set of the whole numbers and their opposites is called integers2>Examples i2clude: -4, -3, -2, -1, 0, 1, 2, 3, 4
The positive and negative integers and fractions are rational numbers2>Examples i2clude: -2, -1.5, -12/3, -1, -3/4, -1/2, 0, 1/2, 3/4, 1, 2, 2.5, 2 3/4
Addition and Subtraction
Students model and symbolize problems to develop meaning and skill in addition and subtraction before developing algorithms.
The colored chip model requires an understanding of opposites.
The number line model helps make the connection to rational numbers as quantities.
Sometimes it is helpful to restate an addition problem as a subtraction or a subtraction problem as an addition.
Example
 One color chip (black) represents positive numbers and another color (red) represents
negative numbers.
One color chip (black) represents positive numbers and another color (red) represents
negative numbers.
Tate owes his sister, Julia, $6 for helping him cut the lawn. He earns $4 delivering papers. Is Tate “in the red” or “in the black”?
Black and red chips on a board represent income and expenses. The result is that he is “in the red” 2 dollars or has -2 dollars. This problem may be represented with the number sentence -6 + 4 = -2.
The number line below models a temperature change from -4°F to +45°F. The sign of the change shows the direction of the change.
-4° + n ° = +45° or -4° + +49° = +45°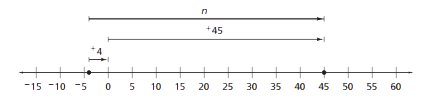
When calculating +12 + -8, the result is the same as if you subtracted +8 in the problem +12 - +8. When calculating +5 - -7, the result is the same as if you added +7 in the problem +5 + +7
Multiplication
Multiplication can be explored by counting occurrences of fixed-size movement along the number line.
Example
If a runner passes the 0 point running to the left at 6 meters per second, where will he be 8 seconds later?
This can be represented as 8 jumps of -6 on the number line.
-6 + -6 + -6 + -6 + -6 + -6 + -6 + -6 = -48 or 8 x -6 = -48
Division
A multiplication fact can be used to write two related division facts.
Example
You know that 5 x -2 = -10. You can write related division sentences: -10 ÷ -2 = 5 and -10 ÷ 5 = -2. By developing division based on its relationship to multiplication, students can determine the sign (positive or negative) of the answer to a division problem.
Order of Operations
Mathematicians have established rules for the order in which operations (+, -, x ÷) should be carried out.
Example
- Compute any expressions within parentheses.
3 + 4 x (6 ÷ 2) x 5 - 72 + 6 ÷ 3 = - Compute any exponents.
3 + 4 x 3 x 5 - 72 + 6 ÷ 3 = - Do all multiplication and division in order from left to right.
3 + 4 x 3 x 5 - 49 + 6 ÷ 3 =
3 + 60 - 49 + 2 = - Do all addition and subtraction in order from left to right.
63 - 49 + 2 =
14 + 2 = 16
Commutative Property
This property does not hold for subtraction or division.
Example
The order of addends does not matter.
5 + 4 = 4 + 5
-2 + 3 = 3 + (-2)
The order of factors does not matter.
5 x 4 = 4 x 5
-2 x 3 = 3 x (-2)
Order does matter in subtraction.
5 - 4 ≠ 4 - 5
-2 - 3 ≠ 3 - (-2)
Order does matter in division.
5 ÷ 4 ≠ 4 ÷ 5
-2 ÷ 3 ≠ 3 ÷ (-2)
Distributive Property
This property is introduced and modeled through finding areas of rectangles.
Example
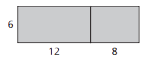
This property shows that multiplication distributes over addition.
6 x (12 + 8) = (6 x 12) + (6 x 8)