7-5 Moving Straight Ahead - Concepts and Explanations
Linear Relationships
A relationship is linear if there is a constant rate of change between the two variables. That is, for each unit change in x, there is a constant change in y.
Tables
In the table, the constant rate of change can be observed as a pattern of consistent change in the variables.
Example
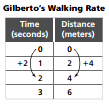
For Gilberto’s walking rate, as the time increases by 1 second, the distance increases by 2 meters. The constant rate of change is 2 meters per second.
Graphs
If we graph the data, the constant rate of change between the two variables shows up as a straight line. This constant rate of change is called the slope of the line. It is the ratio of change between the two variables. For any two points on the line, slope = vertical change/horizontal change.
Example
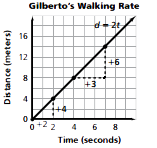
Here, the slope is 4/2 or 6/3 or 2/1.
Equations
In the symbolic representation, the constant rate of change shows up as the coefficient of the independent variable.
Example
Here, the coefficient of t is 2. Gilberto: d = 2t
y-intercept
On a graph, the y-intercept is the point at which the graph of a line crosses the y-axis (vertical axis).
Example
Suppose the cost to rent bikes is $150 plus $10 per bike. Symbolically, we can write
C = 150 + 10n, where C is the cost in dollars and n is the number of bikes. They y-intercept
is at (0, 150) because for 0 bikes, the cost is $150. This means there is a fixed
charge in addition to the cost per bike. The y-intercept is the constant term in the
equation. The slope (or constant rate of change) of the line is 10, the coefficient
of n.
Solving Equations
To solve an equation, students write a series of equivalent equations until it is easy to read the value of the variable. Equivalent equations have the same solutions. Equality is maintained by adding, subtracting, multiplying, or dividing by the same quantity on each side of the equation. For multiplication and division, the quantity must not be zero. These procedures are called the properties of equality
Example
For the equation C = 150 + 10n, if C is 750, what is the value of n?
| Equation | Reason |
|---|---|
| 750 = 150 + 10n | Original equation |
| 750 - 150 = 150 - 150 + 10n | Subtract 150 from each side to undo adding 150 |
| 600 = 10n | Simplify |
| 600/10 = 10n/10 | Divide each side by 10 to undo multiplying by 10 |
| 60 = n | Simplify |
Note that if you replace n with 60 in each step, the equation is true. For example, the original equation simplifies to 750 = 750.