8-2 Looking for Pythagoras - Concepts and Explanations
Finding Area
Students find areas of irregular figures drawn on grids. One method is to subdivide the shape and add the areas of the component shapes. Another method is to enclose the shape in a rectangle and subtract the area outside the figure from the area of the rectangle.
Example
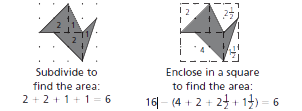
Square Roots
If the area of a square is known, its side length is the number whose square is equal to the area. The side length of a square is not always a whole number. You can use the √ symbol to represent these nonwhole numbers.
Example
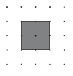
This square has an area of 4 square units. The length of each side is the square root of 4 units, which is equal to 2 units.
Estimating Square Roots
Students develop benchmarks for estimating square roots. Students also estimate square roots with a number line ruler, which helps them to develop a sense of the size of irrational numbers, such as √3, √5, and √7.
Example
√5 is between 2 and 3 because 22 < 5 < 32. It is closer to 2. Try 2.25: 2.252 = 5.0625. So √5 is between 2 and 2.25, but closer to 2.25. Try 2.24: 2.242 = 5.0176. This estimate is even closer. Continue until the desired accuracy is obtained.
Finding Distances
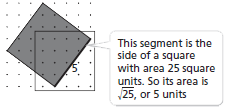
To find various lengths of line segments, students begin by drawing a square that is associated with the length.
Example
Cube Roots
If the volume of a cube is known, its edge length is the number that when multiplied by itself 3 times is equal to the volume. The edge length of a cube is not always a whole number. You can use the 3√ symbol to represent these nonwhole numbers.
Example
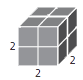
This cube has the volume of 8 cubic units. The length of each edge is the cube root of 8 units, which is equal to 2 units.
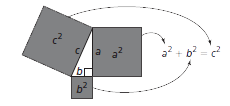
Pythagorean Theorem
In a right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the longest side, called the hypotenuse. Symbolically, this is a2 + b2 = c2, where a and b are the lengths of the legs and c is the length of the hypotenuse.
Example
Finding the Length of a Line Segment
On a grid, you can find the length of a horizontal or vertical line segment by counting the distance. If a segment is not vertical or horizontal, you can treat it as the hypotenuse of a right triangle. You can use the Pythagorean Theorem to find the length of the hypotenuse.
Example
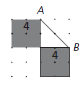The length of line segment AB can be the hypotenuse of a right triangle, c. 22 + 22 = c2, so 4 + 4 = 8 = c2
√8 = c
Irrational and Rational Numbers
An irrational number is a number that cannot be written as a quotient of two integers where the denominator is not 0. Decimal representations of irrational numbers never end and never show a repeating pattern for a fixed number of digits. Rational numbers can be written as a ratio of two integers. Decimal representations of rational numbers terminate or show a repeating pattern.
Example
The numbers √2, √3, √5 and π are examples of irrational numbers. The decimal form of √2 is 1.41421356237.... The decimal part goes on forever without any repeating pattern. The numbers 1/3, -2.7, and √4 are examples of rational numbers.