8-8 Function Junction - Concepts and Explanations
Functions
Formal language and notation associated with the concept of function are introduced, with special attention given to step, piecewise, and polynomial functions.
Example
A taxi cab owner charges his clients a fare based on the following rule: $5.00 for a distance of up to one mile and $2.00 for each additional mile or part of a mile. This rule is an example of a step function.
Sequences
An arithmetic sequence is a sequence of numbers that has a constant rate of change. A geometric sequence is a sequence of numbers that has a constant factor. These sequences can be treated as linear and geometric functions, respectively, and students learn how to express them with rules in both recursive and closed forms.
Example
An example of an arithmetic sequence would be:
s(n) = 1, 4, 7, 10, 13, ...
An example of a geometric sequence would be:
g(n) = 1, 3, 9, 27, 81, ...
Translating and Stretching Functions
Students have previously worked with transformational geometry. In this Unit, students develop the connections between expressions for functions whose graphs are related by translation and one-dimensional stretching/shrinking. Students learn how to determine characteristics of graphs by looking at different forms of the equation.
Example
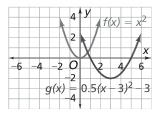
Stretching the graph of f(x) = x2 toward the x-axis by a factor of 0.5, and then translating the graph down two units and to the right three units results in the following graph, whose equation is g(x) = 0.5(x - 3)2 - 2.
Completing the Square
Skill and understanding in the use of completing the square is developed to transform quadratic expressions to equivalent vertex forms.
Example
To put the function f(x) = x2 + 4x - 4 into vertex form, a student could complete the square and obtain f(x) = (x + 2)2 - 8.
Often the vertex form gives us information about the graph of a function that is easier to see than when the function is written in standard form.
Quadratic Formula
The Quadratic Formula is used for solving quadratic equations in the form ax2 + bx + c = 0. The Quadratic Formula is also used to find complex numbers to provide solutions for cases where no real-number solutions exist.
Example

Skill and understanding in the use of completing the square is developed to transform
quadratic expressions to equivalent vertex forms.
Polynomial Functions
Analysis of polynomial functions and their graphs is extended to the study of the connection between expressions and graph properties, and then to develop operations with polynomial functions.
Example
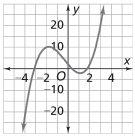
Some functions, called polynomial functions, have graphs that contain “hills” or “valleys” that may not be maxima or minima. These hills and valleys are called local maxima and local minima, respectively. One example is the graph of f(x) = x3 + x2 - 6x + 2.