Let's Be Rational and the CCSSM Algebra
CCSS.MATH.CONTENT.6.EE.A.2.A
Write expressions that record operations with numbers and with letters standing for numbers.For example, express the calculation "Subtract y from 5" as 5 - y.
Writing numeric and symbolic expressions and sentences to represent the operations required to solve problems is one of the most important skills in applied mathematics. Each unit of CMP3 includes many activities that develop understanding and proficiency in work on such modeling tasks.
In Let’s be Rational, there are several places where students are explicitly asked to model a situation with number sentences and equations: Problems 1.3, 1.4, 2.2, 3.1, 3.2, and 4.3. Here we present two of these Problems, 1.4 and 4.3, to demonstrate the unique ways that CMP3 builds students’ skills to model problems with number sentences and with equations containing variables.
Let’s be Rational Problem 1.4
For example, using a Spice Recipe context, Problem 1.4 parts B, C, and D ask students explicitly to write number sentences to model problems of adding and subtraction spices. Then in part E, students use algebraic reasoning to interpret an existing equation and to write a story that would apply to that equation.
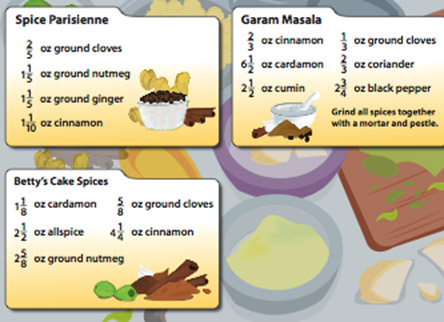
For Question B and C,
- Decide which operation you will use to solve each problem.
- Find an approximate answer using estimation.
- Write a number sentence and answer the question.
B)
- How many ounces of spice does Betty buy?
- Tevin is allergic to cinnamon. If Betty removes cinnamon from the recipe for him, how many ounces of spice does she buy?
C)
Ms. Garza buys spices to make one batch of Garam Masala. When she weighs her spices at home, she only has 10 11/12 ounces of spice. Which spice did Ms. Garza forget?
D)
Renuka has two pounds of pepper in her cupboard. She knows that there are 16 ounces in one pound. After Renuka makes one batch of Garam Masala, how many ounces of pepper does Renuka have left in her cupboard?
E)
For each number sentence below, write a spice story. Then find the value for N that makes the sentence true.
- 3 1/6 - 1 3/4 = N
- N + 3/4 = 1 1/2
- 2 2/3 - N = 1 1/4
Let’s be Rational Problem 4.3
In Problem 4.3 of Let’s Be Rational asks students to analyze five different word problem situations, to decide which operations are needed to solve the problems, and to write one or more expressions that represent those operations.
The exercises involve writing expressions to record problem-solving operations in Let’s Be Rational and result in number sentences like the following, which applies to Part C:
Sasha bought 3 1/2 pints of blueberries to make jelly. She ate 3/4 of a pint of berries on her way home. How many pints of berries does she have left to make jelly?
3 1/2 - 2/4 = 2 3/4 [Let's Be Rational 4.3C]
Understandings and skills used in writing numeric expressions and equations are extended to use of letter names for variables in several other problems of Let’s Be Rational. For example, Problem 4.3H:
H A grandmother is making clothes for her three granddaughters. She will make a jacket and one other item for each granddaughter. The three other items will be exactly the same. A jacket takes 1 5/8 yards of fabric. She has ten yards of material in all. She is trying to figure out how much fabric she has for each of the three extra items.

Let N represent the fabric needed one extra item. Explain why each of the sentences below does or does not describe the situation. (More than one sentence may apply.)
- 3(1 5/8 + N) = 10
- 10 - 4 7/8 = 3N
- 3 x 1 5/8 + N = 10
- 10 ÷ 1 5/8 = N
This problem is answered by the equations 3(1 5/8+N)=10 and 10-4 7/8=3N.
CCSS.MATH.CONTENT.6.EE.A.2.B
Identify parts of an expression using mathematical terms (sum, term, product, factor, quotient, coefficient); view one or more parts of an expression as a single entity. For example, describe the expression 2 (8 + 7) as a product of two factors; view (8 + 7) as both a single entity and a sum of two terms.
The mathematical terms sum, product, factor and quotient are used throughout Let’s Be Rational unit. The term quotient is defined and used in development of fraction division algorithms in Let’s Be Rational Investigation 3.
Investigation 3 Dividing with Fractions
So far in Let's Be Reational, you have solved problems using addition, subtraction and multiplication. In Investigation 3, you will solve problems that require division of fractions. As you work on these problems, think about similarities and differences among the problems.
In the number sentence 21 ÷ 7 = 3, 21 is dividend, 7 is the divisor, and 3 is the result, or quotient.
You can use the vocabulary of division problems as placeholders in a division number sentence. The division sentence below shows how these quantities relate to one another.
dividend ÷ divisor = quotient
First, you need to understand what division of fractions means. Then you can calculate quotients when the divisor or the dividend, or both, is a fraction.
CCSS.MATH.CONTENT.6.EE.A.3
Apply the properties of operations to generate equivalent expressions.For example, apply the distributive property to the expression 3 (2 + x) to produce the equivalent expression 6 + 3x; apply the distributive property to the expression 24x + 18y to produce the equivalent expression 6 (4x + 3y); apply properties of operations to y + y + y to produce the equivalent expression 3y.
Let's be Rational Problem 2.3A
The idea of equivalence comes up throughout CMP3 implicitly during the Summary of lessons as students share equivalent methods to solve problems and their teachers help them to make connections between those problem solutions. CMP3 also explicitly asks students to compare solution strategies in Let’s be Rational Problem 2.3. In each of these strategies, the steps involved in solving the problem are equivalent expressions.
Problem 2.3
A)
- Takoda and Yuri are computing 1/2 x 2 2/3. What is a reasonable estimate for this product?
- Takoda and Yuri each use a different strategy.
Takoda's Strategy
I used what I know about fractions to rewrite 2 2/3 as 8/3 to make the problem easier to solve.
1/2 x 2 2/3 = 1/2 x 8/3
= 8/6
= 1 2/6
= 1 1/3Yuri's Strategy
I wrote 2 2/3 as (2 + 2/3) and used the Distributive Property to make the problem easier to solve.
1/2 x 2 2/3 = 1/2 x (2 + 2/3)
= (1/2 x 2) + (1/2 x 2/3)
= 1 + 2/6
= 1 2/6
= 1 1/3- Does each strategy work? How do you know?
- How are the strategies similar? How are they different?
3. Use both strategies to solve 1 1/3 x 4/5. Then check your answer with a drawing.
CCSS.MATH.CONTENT.6.EE.A.4
Identify when two expressions are equivalent (i.e., when the two expressions name the same number regardless of which value is substituted into them).For example, the expressions y + y + y and 3y are equivalent because they name the same number regardless of which number y stands for.
Let’s be Rational Problem 2.3A
The idea of equivalence comes up again in considering equivalence of fractions and ratios in the Let’s Be Rational unit. For instance, Problem 2.3 (see above) encourages students to compare two strategies for simplifying the multiplication of a fraction and a mixed number. The steps in each solution method are equivalent number sentences.
Let’s be Rational Problem 4.3
Understandings and skills used in writing numeric expressions and equations are extended to use of letter names for variables in several other problems of Let’s Be Rational. In Problem 4.3H (see above), this idea is extended to showing how two equations are equivalent representations of a single problem solution.
CCSS.MATH.CONTENT.6.EE.B.5
Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.
Let’s be Rational Problem 1.2
The general idea of solving inequalities is first introduced informally in Problem 1.2 in Lets’ Be Rational. This informal introduction is anchored in the context of reasoning about overestimates and underestimates.
Sometimes you shouldoverestimate,or give an estimate that is a bit bigger than the actual value. Overestimate to make sure you have enough. Sometimes you shouldunderestimate,or give an estimate that is a bit smaller than the actual value. Underestimate to stay below a certain limit.
For Question A-E,
- Answer the question by using estimation. Explain your reasoning.
- Explain how confident you are in your answer.
- For each estimate you make, tell whether it is an overestimate or an underestimate. Explain why you chose to overestimate or underestimate.
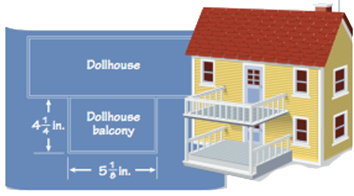
A) Mrs. Edwards is building a dollhouse for her children. She needs to buy wood for the railing on the balcony.
The wood is available in 12-inch, 14-inch, and 16-inch lengths. She does not want to waste wood. What length should she buy?
CCSS.MATH.CONTENT.6.EE.B.6
Use variables to represent numbers and write expressions when solving a real-world or mathematical problem; understand that a variable can represent an unknown number, or, depending on the purpose at hand, any number in a specified set.
Let’s be Rational Problem 1.4E
In Problem 1.4E students are asked to interpret variable equations and write a contextual story that matches the equation.
E) For each number sentence below, write a spice story. Then find the value for N that makes the sentence true.
- 3 1/6 - 1 3/4 = N
- N + 3/4 = 1 1/2
- 2 2/3 - N = 1 1/4
Let’s be Rational Investigation 4
Students’ confidence and ability to work with expressions and equations builds throughout the unit. In Investigation 4 of Let’s be Rational, students use variables to represent numbers and write expressions to solve mathematical and real world problems.This is elaborated further below.
CCSS.MATH.CONTENT.6.EE.B.7
Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all nonnegative rational numbers.
Let’s Be Rational Investigation 4
Several CMP3 units develop student understanding and skill in work with these equations. The key idea in those earlier encounters with equation solving is fact families. For any three numbers a, b, and c, if a + b = c, then we can infer that b + a = c, a = c – b, and b = c – b. Similarly, for any three numbers a, b, and c, if ab = c we can infer that ba = c, a = c ÷ b (b ≠ 0) and b = c ÷ a (a ≠ 0). These relationships can be used to solve any one-step linear equation.
For example, to solven+ 5 = 34 we reason as follows:
If n + 5 = 34, then n = 34 – 5 or n = 29
Checking, we see that 29 + 5 = 35.
Similarly, to solve 5n = 35 we reason as follows:
If 5n = 35, then n = 35 ÷ 5 or n = 7
Checking, we see that 5(7) = 35.
This use of fact families to solve one-step linear equations is developed and practiced in the Let’s Be Rational unit. So students should have efficient and easy to recall strategies for solving x + p = q and px = q before they get to Variables and Patterns.
Let’s be Rational Problem 4.1
Below are two fact families expressing relationships among fractions.
| Example 1 | Example 2 | |
|---|---|---|
| Addition Sentence | 3/4 ÷ 1/8 = 7/8 | 6/8 + N = 7/8 |
| Related Number Sentences |
1/8 ÷ 3/4 = 7/8 7/8 - 3/4 = 1/8 7/8 - 1/8 = 3/4 |
N + 6/8 = 7/8 7/8 - 6/8 = N 7/8 - N = 6/8 |
- How are these fact families different from each other?
- How do you know that the three related sentences below the top row are true?
In Problem 4.1 you will create fact families and use them to find unknown numbers.
A) For each number sentence, write a complete fact family and find the value of N.
- 5/10 - 2/5 = N
- 3 3/5 + 1 2/3 = N
- Describe the relationship between addition and subtraction. Use the fact families in parts (1) and (2) as examples.
B) For each number sentence, find the value N.
- N + 1 2/3 = 5 5/6
- 3/4 + N = 17/12
- N - 1/2 = 3/8
- How can fact families help you find the value of N in parts (1) - (3)?
Let’s be Rational Problem 4.2
Now it is your turn to write fact families.
A)Write a complete fact family for each of the following sentences.
- 2/3 × 1/5=2/15
- 3/4 × 5/8 = 15/32
- 9/40 ÷ 3/5 = 3/8
- 4/15 ÷ 2/5 = 2/3
B) Write a complete fact family for each of the following equations. Use your fact family to find the value of N
- 3/8 × N = 21/80
- 2/3 × N = 10/15
- 1 ÷ N = 2/3
- 8/15 ÷ N = 2/3
C)Marla says she can use the idea of decomposing a product to find the unknown factor, N, in 15 = 2 × N. She rearranges this multiplication sentence as the division sentences 15 ÷ 2 = N. Does Marla's strategy work? Explain why or why not?
D) Below are sets of three numbers. Some of these sets can be related using addition and subtraction. Some can be related using multiplication and division. For each set, identify what the relation is. Then write a complete fact family.
- 3/5, 1/3, 14/15
- 3/4, 4/3, 1
- 1 1/2, 2 2/3, 4 1/6
- 3/2, 3, 9/2
CCSS.MATH.CONTENT.6.EE.B.8
Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
Thorough and explicit attention to solving inequality equations does not formally occur until Variables and Patterns. If there is a need to introduce inequalities earlier than that, problems in Let’s be Rational can be extended to include problems with solutions that can be written using an inequality.
Let’s be Rational Problems 1.2 and 4.3
At the end of Let’s be Rational, following Investigation 4, you may want to revisit the overestimation and underestimation ideas from Problem 1.2 and rewrite these situations as inequalities. Here we present an example using Problem 1.2D, of how this might be accomplished.
D) Jasmine's raspberry jam recipe calls for 4 1/3 quarts of raspberries. She has picked 3 1/2 quarts of raspberries. About how many more quarts of raspberries should she pick?
The following scenario is an example of how this could be revisited and extended to explicitly include solving an inequality:
Teacher: “When we solved this problem, we said that this was an overestimate. Why is that?”
Student: “Because she needs at least 4 1/3quarts of raspberries. If she picks more than that, it is OK, she will just have a little left over. But she cannot pick less than that and still have enough to make her jam."
Teacher: “How might we write this using an inequality statement?”
Student: 3 1/2 + N ≥ 4 1/3